segue anexo
quarta-feira, 22 de maio de 2013
Questão 3.21
Considere o manômetro de dois fluidos mostrado. Calcule a diferença de pressão aplicada.
d=ρ / ρ padrão ρpadrão = ρ H2O = 1000 kg/m³
ρ1 = ρ H2O = 1000 kg/m³
d2= d tetracloreto de carbono = 1,52
ρ2 = 1,52 . 1000 kg/m³ = 1520 kg/m³
ϒ = ρ . g g = 10m/s²
ϒ1 = 1000 kg/m³ . 10m/s² = 10000 N/m³
ϒ1 = 1520 kg/m³ . 10m/s² = 15200 N/m³
l = 10,2 mm = 0,0102 m
p1 + ϒ1.l1 - ϒ2.l2 = p2 l1=l2=l
p1-p2 = - ϒ1.l + ϒ2.l
p1-p2 = (- 10000 N/m³ + 15200 N/m³)0,0102 m
p1-p2 = 53,04 N
Questão 1.18
a) Potencia:
Energia / Tempo = (Força x Distancia)/Tempo = (F.L)/t = N.m/s ou lbf.ft/s
b) Pressão:
Força / Area = F/L² = n/m² ou lbf/ft²
c)Módulo de Elasticidade:
Força / Área = F/L² = N/m² ou lbf/ft²
d) Velocidade angular:
Radianos / Tempo = 1/t = 1/s
e) Energia:
Força x Distancia = F.L = N.m ou lbf.ft
f) Momento de uma força:
Força x Distancia = F.L = N.m ou lbf.ft
g) Quantidade de movimento:
Massa x Velocidade = (M.L)/t
2ª Lei de Newton F=m.a
(Força x Velocidade)/aceleração = (F.(L/t)/(L/t²) = F.t = N.s ou lbf.s
h) Tensão de cisalhamento:
Força / Area = F/L² = N/m² ou lbf/ft²
i) Deformação:
Variação de comprimento / comprimento = L/L = -
Energia / Tempo = (Força x Distancia)/Tempo = (F.L)/t = N.m/s ou lbf.ft/s
b) Pressão:
Força / Area = F/L² = n/m² ou lbf/ft²
c)Módulo de Elasticidade:
Força / Área = F/L² = N/m² ou lbf/ft²
d) Velocidade angular:
Radianos / Tempo = 1/t = 1/s
e) Energia:
Força x Distancia = F.L = N.m ou lbf.ft
f) Momento de uma força:
Força x Distancia = F.L = N.m ou lbf.ft
g) Quantidade de movimento:
Massa x Velocidade = (M.L)/t
2ª Lei de Newton F=m.a
(Força x Velocidade)/aceleração = (F.(L/t)/(L/t²) = F.t = N.s ou lbf.s
h) Tensão de cisalhamento:
Força / Area = F/L² = N/m² ou lbf/ft²
i) Deformação:
Variação de comprimento / comprimento = L/L = -
Questão 3.22
O manômetro mostrado contém dois líquidos. O líquido A tem densidade relativa 0,88 e o líquido B 2,95. Calcule a deflexão, h, quando a diferença de pressão aplicada é p1-p2= 18 lbf/ft².
- Teorema de Stévin
d=ρ / ρ padrão ρpadrão = ρ H2O = 1000 kg/m³
ρA = 0,88 . 1000 kg/m³ = 880 kg/m³
ρB = 2,95 . 1000 kg/m³ = 2950 kg/m³
ϒ = ρ . g g = 10m/s²
ϒA = 880 kg/m³ . 10m/s² = 8800 N/m³
ϒB = 2950 kg/m³ . 10m/s² = 29500 N/m³
p1-p2 = 18 lbf/ft² = 861,845 Pa
p1 + ϒA.hA - ϒB.hB = p2
p1-p2 = - ϒA.h + ϒB.h
861,845 Pa = (- 8800 N/m³ + 29500 N/m³)h
h = 861,845 Pa / 20700 N/m³
h= 0,0416 m
- Teorema de Stévin
d=ρ / ρ padrão ρpadrão = ρ H2O = 1000 kg/m³
ρA = 0,88 . 1000 kg/m³ = 880 kg/m³
ρB = 2,95 . 1000 kg/m³ = 2950 kg/m³
ϒ = ρ . g g = 10m/s²
ϒA = 880 kg/m³ . 10m/s² = 8800 N/m³
ϒB = 2950 kg/m³ . 10m/s² = 29500 N/m³
p1-p2 = 18 lbf/ft² = 861,845 Pa
p1 + ϒA.hA - ϒB.hB = p2
p1-p2 = - ϒA.h + ϒB.h
861,845 Pa = (- 8800 N/m³ + 29500 N/m³)h
h = 861,845 Pa / 20700 N/m³
h= 0,0416 m
Questão 1.2
Conservação da massa:
A massa de um sistema é constante, por definição;
A segunda lei do movimento de Newton:
A força resultante aplicada a um corpo produz uma aceleração a ela diretamente proporcional;
Primeira lei da termodinâmica:
Em um processo termodinâmico fechado, a alteração da energia interna do sistema é igual à diferença entre o alteração do calor acumulado pelo sistema e da alteração do trabalho realizado;
Segunda lei da termodinâmica:
A quantidade de entropia de qualquer sistema isolado termodinamicamente tende a incrementar-se com o tempo, até alcançar um valor máximo;
Principio da quantidade de movimento angular:
O momento angular de um conjunto de partículas em relação a um ponto de referência é definido como a soma do momento angular de todas as partículas em relação a esse ponto.
Questão 2.84
Boa Noite!
A questão 2.34 pede como as asas de um aeroplano desenvolvem sustentação:
A sustentação é a força que sustenta o aeroplano no
ar.
Ela atua na vertical, de baixo para cima; opõem-se à
força da gravidade, ou peso do avião, a outra das quatro forças.
Na sua deslocação no meio atmosférico, a asa funciona como um plano inclinado: A diferença de pressões entre as superfície inferior e superior atira a asa para cima. Contrariamente ao que parece, o impacto da pressão na superfície inferior produz apenas 30% da sustentação.
Na sua deslocação no meio atmosférico, a asa funciona como um plano inclinado: A diferença de pressões entre as superfície inferior e superior atira a asa para cima. Contrariamente ao que parece, o impacto da pressão na superfície inferior produz apenas 30% da sustentação.
Bjooos!
Questão 2.37
Olá!
A questão pede para explicar como um patim interage com a superfície do gelo. Quais os mecanismos agem no sentido de reduzir o atrito de deslizamento entre o patim e o gelo.
Essa ação ocorre graças ao reduzido atrito entre as lâminas do patins e a superfície do gelo.
O peso do patinador, concentrado nas lâminas, exerce uma pressão sobre o gelo derretendo-o e formando uma pequena camada de água entre as lâminas e a superfície do gelo. Dessa forma o atrito torna-se muito pequeno, facilitando o movimento.
Bjoos!
A questão pede para explicar como um patim interage com a superfície do gelo. Quais os mecanismos agem no sentido de reduzir o atrito de deslizamento entre o patim e o gelo.
Essa ação ocorre graças ao reduzido atrito entre as lâminas do patins e a superfície do gelo.
O peso do patinador, concentrado nas lâminas, exerce uma pressão sobre o gelo derretendo-o e formando uma pequena camada de água entre as lâminas e a superfície do gelo. Dessa forma o atrito torna-se muito pequeno, facilitando o movimento.
Bjoos!
Questões 1.1, 2.54, 2.59 e 3.20
1.1
Algumas substâncias comuns são:
Alcatrão areia creme de barbear
Massa
de calafetar gelatina
Argila
para modelar cera pasta
dental
Alguns
desses materiais apresentam características de comportamento sólido e fluido
sob condições diferentes. Explique e dê exemplos.
Isso se dá, devido à
maioria dos fluidos terem comportamento não - newtoniano, onde as substâncias
não seguem a lei de Newton, isto é, a tensão de cisalhamento não é diretamente
proporcional à taxa de deformação.
Exemplos: pasta
dental, creme de barbear, argila para modelar.
2.54
Encha lentamente um copo com água até o nível máximo possível. Observe o nível
da água bem de perto. Explique agora como este nível pode ser superior ao do
copo.
O nível é superior ao
copo, devido a tensão superficial, este efeito físico, leva a superfície a se
comportar como uma membrana elástica que o leva a resistir a tensão de tração.

2.59
Como as asas de um aeroplano desenvolvem sustentação?
A sustentação é uma
força em uma asa (ou qualquer outro objeto sólido) imersa em um fluido em
movimento, e atua de forma perpendicular
ao fluxo do fluido. A força líquida é criada por diferenças de pressão geradas
por variações na velocidade do ar em todos os pontos ao redor da asa. Essas
variações de pressão são causadas pela interrupção e pelo desvio do fluxo de ar
que passa pela asa.
3.20
Considere um manômetro conectado como mostrado. Calcule a diferença de pressão.

Considerações:
-
Fluidos não-newtonianos
-
parte do h dos tubos foram anulados onde possuíam mesma altura e mesmo fluido.
PA –PB = ỵ água
x h água + ỵ benzeno x h benzeno
PB = -470m x 10000kg/m3 + 470 x 87650 kg/m3
PB = 3649550 Pa
sábado, 18 de maio de 2013
Tubos em U
Começamos com dois tubos em forma de U, de secção uniforme S, que é cheio com água, o tubo esquerdo até uma altura h1e o tubo direito até uma altura h2, tal como é mostrado na figura.

A seguir, conectamos ao extremo direito do tubo esquerdo, e o extremo esquerdo do tubo direito, com outro tubo de mesma secção. Temos uma coluna de ar a pressão atmosférica Pa (em cor amarela) encerrada entre as superfícies livres de alturas h1e h2 dos dois ramas mais próximos dos tubos em forma de U.
O comprimento da coluna de ar é La=H-h1-h2+d. Sendo H a altura dos tubos em U, e d a separação entre os mesmos, tal como é mostrado na figura

Adicionamos um volume V=S·x de água no ramo esquerdo do primeiro tubo, e observamos os níveis da água nos ramos dos dois tubos, o volume e a pressão da coluna.
Resolução do sistema de equações
Os dados do problema são:
As alturas iniciais do líquido nos dois ramos do tubo em U são
- a esquerda h1.
- a direita h2.
- Comprimento inicial da coluna de ar La
- Pressão inicial do ar na coluna Pa=1.013·105 Pa
- Volume de líquido S·x que é adicionado ao ramo esquerdo do primeiro tubo em U.

As incógnitas são as alturas do líquido em cada ramo dos dois tubos em forma de U
- esquerda do primeiro tubo, h1i
- direita do primeiro tubo, h1d
- esquerda do segundo tubo, h2i
- direita do segundo tubo, h2d
- Comprimento final da coluna Lf
- Pressão final da coluna Pf
Para resolver o problema, temos que resolver um sistema de 6 equações com 6 incógnitas.
- Se considerarmos a água como fluido incompressível, teremos que
- O comprimento final do líquido no segundo tubo em U não mudará
h2i+h2d=2h2 (1)
- Ao primeiro tubo acrescentamos um comprimento x de água, e pela mesma razão se cumprirá que
h1i+h1d=2h1+x (2)
- Ao estar o fluido em equilíbrio, coincidirão as pressões na origem pelo ramo esquerda do primeiro tubo devidas a atmósfera Pa e a coluna de líquido de altura h1i e pelo ramo direito devidas a pressão Pf da coluna de ar e a altura da coluna de líquido h1d. Se ρ é a densidade da água, e g a aceleração da gravidade a equação fundamental da estática de fluidos é escrita:
Pa+ρgh1i=Pf+ ρgh1d (3)Coincidirão também as pressões na origem pelo ramo direito do segundo tubo devidas a atmósfera Pa e a coluna de líquido de altura h2d e pelo ramo esquerdo devidas a pressão Pf da coluna de ar e a altura da coluna de líquido h2iPa+ρgh2d=Pf+ ρgh2i (4)
- A coluna de ar tem uma pressão inicial Pa e um volume inicial S·La, uma pressão final Pf e um volume final S·Lf. Supondo uma transformação isotérmica entre os dois estados, temos
Pa·La=Pf·Lf (5)
- Finalmente, uma consideração geométrica. O comprimento combinada da água e da coluna de ar na secção central dos dois tubos em forma de U permanece constante.
h1+h2+La=h1d+h2i+Lf. (6)
Solução do sistema de equações
Para resolver o sistema de seis equações com seis incógnitas, são combinadas as equações do seguinte modo.
Somamos as equações (3) e (4)
2Pa+ρg(h1i+h2d)=2Pf+ ρg(h1d + h2i) (7)
Explicitamos Pf na equação (5) e substituimos na (7)
Somamos as equações (1), (2) e (6)
h2i+h2d+h1i+h1d + h1+h2+La =2h2+2h1+x+ h1d+h2i+Lf.
h1i+h2d=h2+h1+x+Lf-La (9)
Na equação (6) explicitamos h1d+h2i
h1d+h2i= h1+h2+La-Lf (10)
Substituímos (9) e (10) em (8) e escrevemos Pa=ρgL0. L0 é a altura da coluna de água, cuja pressão na base equivale a pressão atmosférica. Tomando água como líquido manométrico em vez de mercúrio na experiência de Torricelli.
Nos resta a seguinte equação de segundo grau em Lf.
Cuja solução é
Conhecida Lf calculamos Pf na equação (5)
Na equação (3) explicitamos h1i- h1d que com a equação (2) forma um sistema de duas equações com duas incógnitas.
h1i+h1d=2h1+x (2)
Somando e subtraindo membro a membro ambas as equações despejamos h1i y h1d
 (12)
(12)
Na equação (4) explicitamos h2d- h2i que com a equação (1) forma um sistema de duas equações com duas incógnitas.
h2i+h2d=2h2 (1)
Somando e subtraindo membro a membro ambas equações explicitamos h2d y h2i
 (13)
(13)
Exemplo:
Dados
- Altura dos tubos H=1.0 m.
- Separação d=0.2 m
- Densidade da água ρ=1000 kg/m3
- Pressão atmosférica Pa=1.013·105 Pa. Por que L0=10.34 m, altura da coluna de água cuja pressão na base equivale a pressão atmosférica.
- Aceleração da gravidade g=9.8 m/s2
Com o ponteiro do mouse arrastamos as flechas até fazer com que a altura inicial da água em ambos os ramos:
- do primeiro tubo seja h1=0.25 m
- do segundo tubo seja h2=0.45 m
Com estes dados determinamos o comprimento inicial da coluna de ar La= H-h1-h2+d=1.5 m.
Suponhamos que acrescentamos um volume de água ao ramo esquerdo do primeiro tubo, que equivale a uma altura x=0.88 m. Calculamos as incógnitas
Da expressão (11) calculamos o comprimento final da coluna de ar
Da equação da transformação isotermica (5) calculamos a pressão final Pf
1.013·105·1.5=Pf·1.45 Pf=1.05·105 Pa.
O incremento de pressão foi de ΔP=Pf-Pa=3783 Pa
As fórmulas (12) nos dão os valores das alturas finais de água em ambos ramos do primeiro tubo h1i e h1d

As fórmulas (13) nos dão os valores das alturas finais de água em ambos os ramos do segundo tubo h2i e h2d

Fonte: http://www.sc.ehu.es/sbweb/fisica/fluidos/estatica/tubos_u/tubos_u.htm
Experiência de Torricelli
Para medir a pressão atmosférica, Torricelli empregou um tubo longo, fechado por um de seus extremos, encheu com mercúrio e mergulhou a extremidade aberta numa vasilha de mercúrio. O mercúrio desceu até uma altura h=0.76 m ao nível do mar. Dado que o extremo fechado do tubo e acima da superfície livre do mercúrio se encontra quase no vácuo p=0 (na realidade a pressão de vapor do mercúrio que é pequena), e sabendo a densidade do mercúrio é 13.55 g/cm3 ó 13550 kg/m3 o valor da pressão atmosférica é
 Fonte: http://www.sc.ehu.es/sbweb/fisica/fluidos/estatica/ecuacion/ecuacion.htm |
quinta-feira, 16 de maio de 2013
Lançamento de foguete!
Oi,
Achei um vídeo de projeto para lançamento de foguete!
O nosso vai ser braço hidráulico, mas podemos dar uma olhadinha nesse :D
http://www.youtube.com/watch?feature=player_embedded&v=0qzOzjRJpaU#!
Teorema de Pascal
Segundo o teorema de Pascal, quando aplica-se força à um fluído, confinado em um recipiente, a pressão gerada distribui-se integralmente em todas as direções e sentidos.
Uma aplicação simples deste conhecimento é utilizado no macaco hidráulico, o que torna possivel levantar um automóvel de mais de uma tonelada, aplicando-se uma pequena força em uma alavanca.
Equações básicas.
As equações básicas em uso na mecânica dos fluidos são:
- O princípio da continuidade (ou princípio de conservação da massa)
- A segunda lei do movimento de Newton (ou princípio de conservação do momento linear)
- O princípio de conservação do momento angular
- A primeira lei da termodinâmica (ou princípio da conservação da energia)
- A segunda lei da termodinâmica
Em alguns problemas, pode ser necessário lançar mão de equações que descrevam propriedades físicas do fluido sob estudo. Por exemplo, se este for um gás, pode-se utilizar a equação de estado do gás ideal ( ).
).
 ).
).Métodos de descrição
Em situações onde é fácil identificar e seguir elementos isolados, pode-se usar o método de descrição Lagrangeano, onde as equações são aplicadas a cada elemento individualmente, e o fluido sob estudo é considerado como o conjunto desses elementos individuais (partículas) em movimento. Caso contrário, é mais fácil empregar o método de descrição Euleriano, onde se considera o fluido como um conjunto de pontos no espaço, cada ponto possuindo um conjunto de propriedades variantes no tempo. O método Euleriano trata o fluido como um meio contínuo e utiliza na análise, portanto, a teoria matemática dos campos.
O fluido como um meio contínuo
Apesar de sua natureza molecular, os fluidos podem geralmente ser tratados como meios contínuos. Em um meio contínuo, as propriedades (densidade, velocidade, temperatura, etc.) variam continuamente de um ponto a outro. Esse modelo falha apenas quando as dimensões lineares do problema aproximam-se da ordem de magnitude do caminho médio das moléculas (por exemplo, em gases extremamente rarefeitos).
As propriedades de um ponto podem variar também no tempo. Assim, a representação completa de uma propriedade qualquer  é dada por:
é dada por:  . Se as propriedades do fluido não variam no tempo, o fluxo é dito estacionário. Sob fluxo estacionário, obviamente,
. Se as propriedades do fluido não variam no tempo, o fluxo é dito estacionário. Sob fluxo estacionário, obviamente,  e pode-se escrever
e pode-se escrever  .
.
 é dada por:
é dada por:  . Se as propriedades do fluido não variam no tempo, o fluxo é dito estacionário. Sob fluxo estacionário, obviamente,
. Se as propriedades do fluido não variam no tempo, o fluxo é dito estacionário. Sob fluxo estacionário, obviamente,  e pode-se escrever
e pode-se escrever  .
.
O conjunto de valores de uma propriedade ao longo do fluido constitui um campo, que pode ser escalar ou vetorial, dependendo do caráter escalar ou vetorial da propriedade. Densidade é um exemplo de propriedade escalar; velocidade é um exemplo de propriedade vetorial.
A velocidade de cada ponto pode, em alguns casos de interesse, não variar de acordo com uma ou duas das dimensões do problema. O fluxo é, então, classificado como unidimensional, bidimensional ou tridimensional, dependendo do número de dimensões requeridas para especificar totalmente o campo de velocidades.
Tensões
Uma força  , aplicada sobre uma superfície
, aplicada sobre uma superfície  , num dado ponto
, num dado ponto  , pode ser decomposta em três componentes mutuamente ortogonais: uma normal (
, pode ser decomposta em três componentes mutuamente ortogonais: uma normal (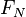 ) e duas tangenciais (
) e duas tangenciais ( e (
e ( )) à superfície. Essas forças darão origem a tensões que podem ser escritas da seguinte maneira:
)) à superfície. Essas forças darão origem a tensões que podem ser escritas da seguinte maneira:
 , aplicada sobre uma superfície
, aplicada sobre uma superfície  , num dado ponto
, num dado ponto  , pode ser decomposta em três componentes mutuamente ortogonais: uma normal (
, pode ser decomposta em três componentes mutuamente ortogonais: uma normal (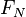 ) e duas tangenciais (
) e duas tangenciais ( e (
e ( )) à superfície. Essas forças darão origem a tensões que podem ser escritas da seguinte maneira:
)) à superfície. Essas forças darão origem a tensões que podem ser escritas da seguinte maneira:
A descricão completa do campo de tensões pode ser obtida tomando-se três superfícies mutuamente ortogonais,  ,
,  e
e  , o que dará origem a um total de nove tensões escalares:
, o que dará origem a um total de nove tensões escalares: 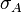 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , onde o primeiro subscrito indica a superfície de referência escolhida e o segundo, a direção considerada no espaço tridimensional. Num sistema de coordenadas cartesianas, é útil orientar as superfícies de referência de modo que sejam perpendiculares aos eixos coordenados. As tensões em um determinado ponto podem, então, ser representadas pela matriz
, onde o primeiro subscrito indica a superfície de referência escolhida e o segundo, a direção considerada no espaço tridimensional. Num sistema de coordenadas cartesianas, é útil orientar as superfícies de referência de modo que sejam perpendiculares aos eixos coordenados. As tensões em um determinado ponto podem, então, ser representadas pela matriz
 ,
,  e
e  , o que dará origem a um total de nove tensões escalares:
, o que dará origem a um total de nove tensões escalares: 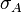 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , onde o primeiro subscrito indica a superfície de referência escolhida e o segundo, a direção considerada no espaço tridimensional. Num sistema de coordenadas cartesianas, é útil orientar as superfícies de referência de modo que sejam perpendiculares aos eixos coordenados. As tensões em um determinado ponto podem, então, ser representadas pela matriz
, onde o primeiro subscrito indica a superfície de referência escolhida e o segundo, a direção considerada no espaço tridimensional. Num sistema de coordenadas cartesianas, é útil orientar as superfícies de referência de modo que sejam perpendiculares aos eixos coordenados. As tensões em um determinado ponto podem, então, ser representadas pela matriz
que é chamada um tensor. O campo de tensões, assim, é um campo tensorial.
Se o ponto  tiver as coordenadas
tiver as coordenadas  , um elemento de volume
, um elemento de volume  nessa posição será limitado pelos seis planos
nessa posição será limitado pelos seis planos
 tiver as coordenadas
tiver as coordenadas  , um elemento de volume
, um elemento de volume  nessa posição será limitado pelos seis planos
nessa posição será limitado pelos seis planos
Esses planos recebem os nomes de plano X negativo, plano X positivo, plano Y negativo, plano Y positivo, plano Z negativo e plano Z positivo, respectivamente. Por convenção, uma tensão  terá valor positivo quando sua direção (dada pelo segundo subscrito) e o plano onde ela atua forem ambos positivos ou ambos negativos. Por exemplo:
terá valor positivo quando sua direção (dada pelo segundo subscrito) e o plano onde ela atua forem ambos positivos ou ambos negativos. Por exemplo:  positiva representa uma tensão no sentido do eixo X aplicada ao plano Y positivo ou uma tensão no sentido contrário ao eixo X aplicada ao plano Y negativo.
positiva representa uma tensão no sentido do eixo X aplicada ao plano Y positivo ou uma tensão no sentido contrário ao eixo X aplicada ao plano Y negativo.
 terá valor positivo quando sua direção (dada pelo segundo subscrito) e o plano onde ela atua forem ambos positivos ou ambos negativos. Por exemplo:
terá valor positivo quando sua direção (dada pelo segundo subscrito) e o plano onde ela atua forem ambos positivos ou ambos negativos. Por exemplo:  positiva representa uma tensão no sentido do eixo X aplicada ao plano Y positivo ou uma tensão no sentido contrário ao eixo X aplicada ao plano Y negativo.
positiva representa uma tensão no sentido do eixo X aplicada ao plano Y positivo ou uma tensão no sentido contrário ao eixo X aplicada ao plano Y negativo.Elasticidade
Uma propriedade importante de um fluido compressível é o seu módulo de elasticidade volumétrica, que indica como o volume específico varia com a pressão aplicada:

Quanto maior o valor de ε, menos compressível é o fluido. O sinal negativo é necessário, uma vez que o volume diminui com o aumento de pressão.
Fonte: http://pt.wikibooks.org/wiki/Mec%C3%A2nica_dos_fluidos/Equa%C3%A7%C3%B5es_b%C3%A1sicas_e_utilizando_as_ferramentas_matem%C3%A1ticas_corretas
Assinar:
Postagens (Atom)


